Lũy Thừa – Xơi Nhanh Để Đạt Điểm Cao Trong Đề Thi Đại Học

Những năm gần đây, môn toán đang có nhiều điểm hết sức biến động. Từ năm 2017 trở đi, bộ giáo dục đã chuyển hình thức thi từ tự luận sang trắc nghiệm. Điều này đã làm cho nhiều học sinh vô cùng hoang mang, lo lắng, không biết phải ôn tập như thế nào cả. Phụ huynh thì lo sốt vó vì không biết liệu rằng hình thức thi như thế này có ảnh hưởng gì đến con mình không hay con mình đã học yếu mà giờ còn chuyển đổi hình thức thi nữa thì phải làm sao. Tuy nhiên các bậc phụ huynh và các em học sinh cũng đừng lo về điều này, bởi dù cho thi tự luận hay trắc nghiệm thì kiến thức vẫn như vậy. Do đó chỉ cần các em học sinh nắm chắc kiến thức thì không phải lo sợ gì cả. Do đó quý bậc phụ huynh và các em học sinh cứ an tâm! Mặc dù là trắc nghiệm nhưng vẫn có sự phân chia giữa các câu dễ và câu khó giống như thi tự luận. Chính vì thế, nếu như muốn điểm cao thì học sinh cần phải nắm vững các phần cơ bản nhất để không phải bị mất điểm những câu dễ. Một trong những phần các em học sinh cần chú ý để lấy điểm là lũy thừa.

Lũy thừa và các dạng toán liên quan

Một định nghĩa hết sức đơn giản, lũy thừa bậc n là tích n thừa số a kí hiệu an =a.a.a…a ( n lần a). Đây là kiến thức chúng ta đã được học ở lớp 6 và được nhắc lại khi chúng ta lên học 12. Tuy nhiên giờ đây khi đã là học sinh 12 thì ta sẽ học nâng cao thêm một bậc, đó là biểu thức lũy thừa và logarit. Cũng giống như lớp 6, biểu thức lũy thừa chính là các phép tính liên quan đến lũy thừa nhưng khi lên 12 các em sẽ được học kĩ hơn. Đồng thời có thê hàm số mũ logarit. Đây là một phần kiến thức chắc chắn sẽ ra trong đề thi đại học và thường đây là những câu cho điểm của đề thi đại học. Do đó muốn đạt điểm cao đại học thì các em cần phải nắm chắn những phần này.

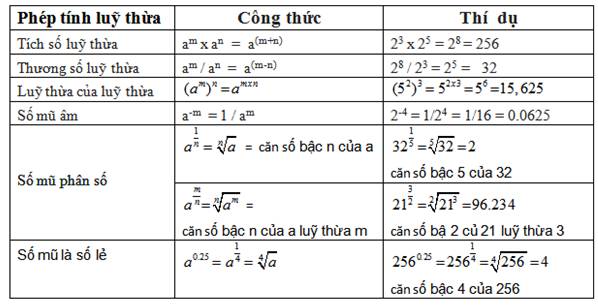
Để làm đươc những dạng toán liên quan đến lũy thừa và logarit ta thường có 2 cách: Theo phương pháp truyền thống, học thuộc công thức, giải nhiều bài tập để nhớ dạng và giải quyết nhanh chúng trong đề thi. Cách thứ hai thì hiện đại, nhanh hơn và dễ hiểu hơn nhiều, đó là sử dụng phương pháp giải toán bằng máy tính cầm tay casio. Đây là phương pháp được áp dụng khá nhiều trong những năm gần đây. Vì phương pháp truyền thống đôi khi có thể gây một số khó khăn cho học sinh trong lúc thi trắc nghiệm: dễ quên công thức mà nếu quên thì phải chịu mất điểm cả câu vì thi trắc nghiệm chỉ chấm đáp án; không có khả năng loại trừ đáp án sai hay không tăng được xác suất chọn đúng đáp án. Tuy nhiên khi áp dụng phương pháp giải toán bằng máy tính cầm tay thì các em học sinh không cần phải lo điều này. Bạn không cần nhớ bất cứ công thức gì cả hay lo đáp án mình khoanh bừa không chính xác hoặc sơ sót lúc làm bài làm mất điểm không chính xác. Việc duy nhất là học sinh chỉ cần bỏ ra 15 phút để học cách bấm máy và khi vào thi chỉ cần 30 giây để giải quyết mọi dạng toán liên quan đến lũy thừa va logarit. Tuy nhiên, không phải ai cũng dạy bạn phương pháp này. Nhiều gia sư vẫn còn dạy theo phương pháp truyền thống làm cho học sinh chậm phát triển, khó hiểu. Do đó bạn cần tìm một trung tâm gia sư chất lượng, uy tín, giàu kinh nghiệm và luôn bắt kịp với thời đại

Cùng gia sư Hà Nội giúp con bạn tiến bộ nhanh chóng

Đội ngũ gia sư Toán của trung tâm được tuyển chọn và đào tạo rất kĩ càng. Do đó gia sư của trung tâm ngoài có kiến thức vững chắc ra thì còn có các kĩ năng giảng dạy cần thiết. Ngoài ra, gia sư còn rất giỏi giao tiếp với học sinh, quan tâm sâu sắc đến học sinh. Không những vậy, khả năng nắm bắt tâm lý của học sinh của gia sư rất tốt, điều này giúp cho học sinh không bị nhàm chán, áp lực hay chán ghét môn học.

Đặc biệt hơn cả gia sư của chúng tôi luôn tích cực thay đổi để theo kịp với thời đại và luôn nghiên cứu, thay đổi phương pháp dạy và giải toán để giúp học sinh có thể đạt kết quả học tập tốt nhất. Chúng tôi tin rằng với phương pháp giảng dạy mới này sẽ giúp các em giải nhanh mọi bài lũy thừa trong đề thi đại học mà không cần tốn công sức.

Vậy bạn còn chần chờ gì nữa mà không ghé thăm website https://giasuviet.net.vn/ của chúng tôi ngay để biết thêm thông tin chi tiết và tìm gia sư giỏi cho con bạn kèm riêng tại nhà.